Let me tell you something you already know. GAN ain’t all sunshine and rainbows.
Today, “GANKIN: generating Kin faces using disentangled GAN” is published in Springer, the article takes a different approach towards solving a complex generating problem: Generating Kins Faces from Parents faces.
In the article, we took a modular and reusable path which made the whole process much easier and less time consuming. In this post, we will discuss a couple of challenges we had with the more typical conditional GAN path. You can also check more samples generated by the model here.
The problem
When building any GAN network, the key is the perfect equilibrium between the generator and the discriminator, sometimes a symmetric design like in DCGAN is enough to maintain the required equilibrium. But what should you do if the problem can’t have a symmetric model? Like in our case, kinship generation? And what if you want to add more attributes that makes the model harder to train?
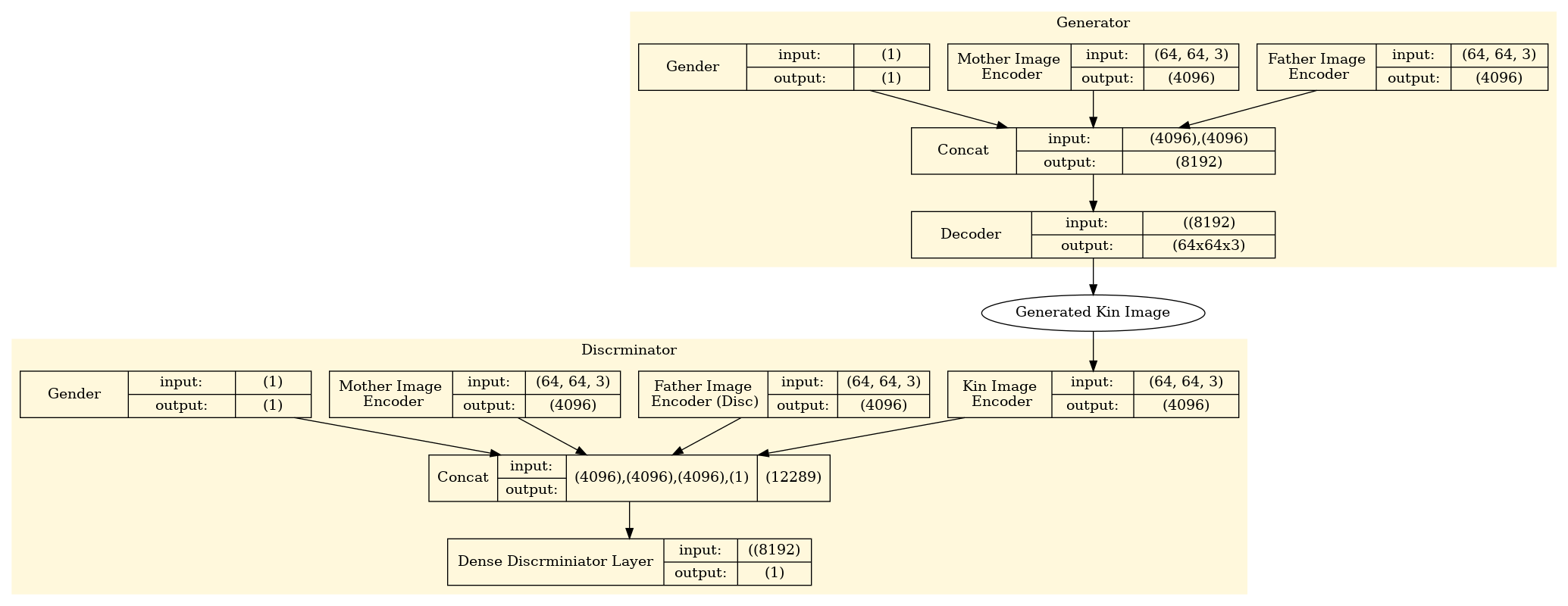
Conditional GAN: Figure 1
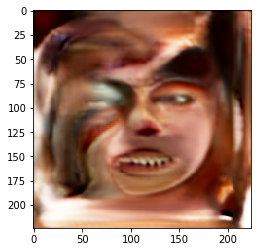
When we had this problem in hand, we started building a new conditional GAN network to generate the kin faces, a rough representation of the network is in figure 1. Once the network was in place, we started running into problems, from diminished gradients to mode-collapse (Figure 2). Although the path at the end of our trials seemed more promising but some questions started to arise that forced us to choose a much different path, What if we wanted to add a new attribute to the input of the generator? What if we wanted to progress to a higher resolution? and more and more what ifs. The majority of the answers were “We will need to painfully retrain the whole model again.
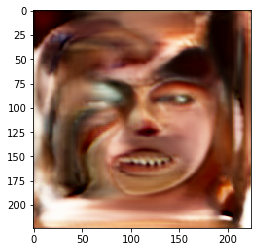
Figure 2
The Solution
The solution that gave us much better results in less time was what we can call the reverse engineering of the latent vector of a pre-trained unconditional GAN (In our case PGGAN). Before diving any deeper, check the table below to have glimpse on the used pipeline in the published paper:
|
Module |
Input | Output | Dataset |
|
Feature Extraction FaceNet |
|
|
VGGFace2 |
|
Kin Features Prediction Neural Network |
|
|
FIW |
|
Feature-to-noise Network Regression |
|
|
100,000 Randomly generated outputs from PGGAN |
| Face Image Generator
PGGAN |
|
|
CelebA |
So in short:
- Feature extraction model: This model should extract the necessary features from the input whatever these features are.
- Features prediction model: After extracting the features of the input, we need to run these features by a network that can predict the features of the needed output. Just the features not the sample itself.
- Feature to noise regression model: Although we used simple regression model, I recommend using a neural network regression model, it will give much better results. This model should take the predicted features alongside all extra features and output the needed latent vector
- Unconditional GAN: Now, all you need to do is to pass the latent vector through an unconditional GAN to get the desired output.
This pipeline is much simpler and can be tested in a matter of days (or hours) not weeks like in the case of conditional GAN, also, the modular nature of the pipeline allows building, training and validating each step separately. The next table shows some typical changes we considered while working on the pipeline and the much of easiness introduced by the pipeline to accomplish each of these changes.
| Change | Pipeline Requirement | Conditional GAN Requirements | Winner |
| Add new attribute like age or gender (Input Change) | Retrain the Linear Regression model and the feature-to-noise model | Complete retrain with a dataset that has all required attributes | The Modular GAN |
| Generate baby faces (Output change) | Retrain the PGGAN on baby faces and retrain the feature-to-noise network. | Complete retrain with a new dataset. | The Modular GAN |
| Add new layers or try new models | Retrain/replace only a sub-model | Complete retrain of the whole network | The Modular GAN |
Anyways, before becoming very optimistic, this won’t work with all types of problems. So, you need to visualize the difference between unconditional GANS (that take only a latent vector) and conditional GANs (that take one or more attributes).
Unconditional GAN can be visualized as a single static infinite manifold of points where each point represent a sample and you try your best to pick the best sample for the inputs. As the manifold is static, you can only change the input to get a different sample, however, conditional GAN has a dynamic infinite manifolds, where attributes controls the manifold itself. In a sense that the output is morphed or transferred from the input. Wherein the unconditional GAN, the output is a randomly selected sample of a static manifold.
If you have any questions, don’t hesitate to ask in the comments section below.












0 Comments